Hola queridos estudiantes, a continuación les dejo la temática LA ELECTRICIDAD: APLICACIONES DE LA LEY DE OHM Y LA LEY DE JOULE, Al final de esta entrada encontraran una actividad para realizar, la cual deberán enviar por correo electrónico, tomando fotografías de su trabajo para adjuntar como archivo, por favor poner en el asunto del correo su nombre completo, el número de la actividad y el grado al cual pertenece, el correo para recibir sus trabajos es profecarito2017periodo2@gmail.com la fecha de entrega de la presente actividad es el día 7 de octubre de 2020.

Carol Ramírez le está invitando a una reunión de Zoom programada.

Tema: CLASE GRADO UNDÉCIMO 30 DE SEPTIEMBRE

Hora: 30 sep 2020 03:30 PM Bogotá

Unirse a la reunión Zoom

https://us04web.zoom.us/j/73808767165?pwd=NTF4djdzd2hmUk82aGpjdWFYcHg3dz09

ID de reunión: 738 0876 7165

Código de acceso: 5Gmeg6

APLICACIONES DE LA LEY DE OHM Y LA LEY DE JOULE

¿Qué es la ley de Ohm?

La ley de Ohm relaciona las tres magnitudes fundamentales de cualquier circuito de corriente continua: la intensidad, la tensión o voltaje y la resistencia.

Se llama así ya que fue descubierta por el físico alemán Georg Ohm.

Georg Ohm descubrió que a una temperatura constante, la corriente eléctrica que fluye a través de una resistencia lineal fija es directamente proporcional al voltaje aplicado a través de ella, y también inversamente proporcional a la resistencia:

Fórmula de la ley de Ohm

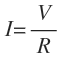ley de ohm ejercicios Donde:

I: Es la intensidad o corriente, medida en amperios (A)
V: Es el voltaje o tensión, medido en voltios (V)
R: Es la resistencia, medida en ohmios (Ω)

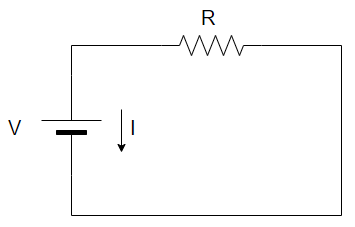
ejercicios de la ley de ohm

La ley de Ohm se utiliza para resolver circuitos, en cálculos electrónicos, por lo que es muy importante entender y recordar su fórmula.

Cualquier dispositivo o componente eléctrico que obedezca la ley de Ohm, es decir, que la corriente que fluye a través de él es proporcional al voltaje que lo atraviesa, tales como resistencias o cables, se dice que son óhmicos o lineales. Los elementos que no lo hacen, tales como transistores o diodos, se dice que son dispositivos no óhmicos.

Usando la Ley de Ohm podemos ver que con un voltaje de 1 V, aplicado a una resistencia de 1 Ω hará que circule una corriente de 1 A.

Cuanto mayor sea el valor de resistencia, menor será la corriente que fluya para un voltaje aplicado dado, ya que ambas magnitudes son inversamente proporcionales:

Por otro lado, la tensión y la intensidad son directamente proporcionales, por lo que si aumenta una, aumenta también la otra:

Conociendo dos valores cualesquiera de las magnitudes de tensión, corriente o resistencia podemos usar la ley de Ohm para encontrar el tercer valor que nos falte.

Ley de Ohm para calcular la intensidad

Si conocemos la tensión y la resistencia, pero no conocemos la intensidad, tan solo tenemos que sustituir V y R por sus valores en la fórmula y operar, ya que en la fórmula tenemos la intensidad despejada:

ley de ohm

Por ejemplo:

En el siguiente circuito, el valor de la tensión es de 230 V y el valor de la resistencia es igual a 100 Ω, ¿qué valor tiene la corriente que circula por el circuito?

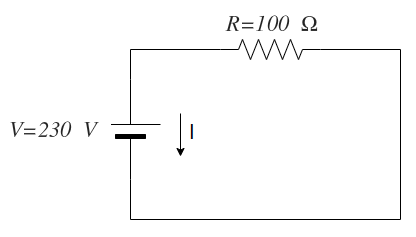
ejercicios resueltos ley de ohm

En este caso conocemos los valores de la tensión y la resistencia:

Para calcular la corriente que circula por el circuito, sustituimos la tensión y la resistencia por sus valores en la fórmula de la ley de Ohm y operamos:

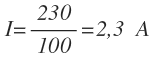
ley de ohm ejercicios resueltos

La intensidad que pasa por la resistencia es igual 2,3 Amperios.

Ley de Ohm para calcular el voltaje

Si conocemos la intensidad y la resistencia y queremos calcular el voltaje, en primer lugar debemos despejar V en la fórmula, pasando la R multiplicando al miembro contrario de la ecuación, ya que está dividiendo :

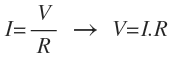
ley de ohm aplicaciones

Una vez despejada la V, ya podemos sustituir los valores de I y R y operar.

Por ejemplo:

Con la piel húmeda, la resistencia del cuerpo humano es de 2500 Ω. ¿Qué tensión sería suficiente para provocar en estas condiciones el paso de una corriente peligrosa de 30 mA por el cuerpo humano?

En este caso conocemos la resistencia y la intensidad:

Podemos calcular la tensión mediante la fórmula:

Para que la tensión esté en voltios, la resistencia debe estar en ohmios y la corriente en amperios. La resistencia ya la tenemos en ohmios, pero la corriente está en miliamperios, por lo que antes de utilizarla en la fórmula de la ley de Ohm, debemos pasar los mA a A, dividiendo entre 1000:

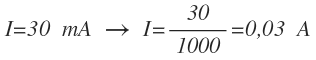
ejercicios de la ley de ohm resueltos

Ahora ya podemos sustituir la resistencia y la intensidad por sus valores en la fórmula y operar:

Sería suficiente una tensión de 75 V.

Ley de Ohm para calcular la resistencia

Cuando conocemos la tensión y la intensidad podemos calcular la resistencia por medio de la ley de Ohm, sólo tenemos que despejar R en la fórmula. Para ello, R pasa multiplicando al primer miembro e I pasa dividiendo al segundo miembro:

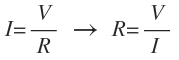
ejercicios de circuitos electricos resueltos ley de ohm

Una vez tenemos R despejada, ya se puede sustituir los valores de V y de I y operar.

Por ejemplo:

Calcula la resistencia del filamento de una lámpara, sabiendo que si la sometemos a una tensión de 125 V, al medir la corriente con un amperímetro obtenemos una intensidad de 0,5 A.

Nos dan los valores de tensión y corriente:

Despejamos R en la fórmula de la ley de Ohm, sustituimos V e I por sus valores y operamos:

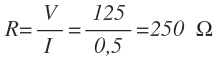
ejercicios con la ley de ohm

El filamento de la lámpara tiene una resistencia de 250 Ω

Ejercicios resueltos de la ley de Ohm

Vamos a resolver unos ejercicios aplicando la ley de Ohm.

Ejercicio 1

La luna térmica de un automóvil consume 3 A con una tensión de 1 V. ¿Qué resistencia tiene dicha luna?

En este problema conocemos I y V y nos piden calcular R.

Despejamos R:

aplicacion de la ley de ohm en circuitos electricos

Sustituimos V e I por sus valores y operamos:

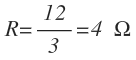
ejercicios de resistencia electrica resueltos ley de ohm

Ejercicio 2

En un conductor circula una intensidad de 4 A y tiene una resistencia de 2 ohmios. ¿Qué tensión tendrá en los extremos?

Conocemos I y R y nos preguntan V.

Primero despejamos V:

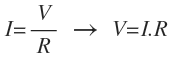
aplicacion de la ley de ohm

Sustituimos y operamos:

LEY DE JOULE

Efecto Joule: El efecto Joule es un término comúnmente usados para referirse a cualquiera de los diferentes efectos físicos descubiertos o caracterizados por el físico inglés James Prescott Joule. Estos efectos físicos no son los mismos, pero todos se mencionan ocasionalmente en la literatura como "efecto Joule" o "ley Joule". Estos efectos físicos incluyen: la primera ley de Joule, una ley física que expresa la relación entre el calor generado y corriente que fluye a través de un conductor. La segunda ley de Joule que declara que la energía interna de un gas ideal es independiente de su volumen y presión, dependiendo solo de su temperatura.

Unidad: Julios
Símbolo: E
Formula: E = R · I² · t

¿Qué es el efecto Joule?

Es el efecto que se da cuando en un conductor donde circula electricidad, parte de la energía cinética que tienen los electrones se transforma en calor por el choque de los electrones con las moléculas del conductor.

El efecto Joule fue descubierto por James Prescott Joule y es también conocido con el nombre de calentamiento resistivo u óhmico, el cuál describe el proceso en el cual la energía que posee una corriente eléctrica se puede transformar en calor conforme fluye por medio de una resistencia.
En particular, cuando la corriente eléctrica fluye a través de un sólido o líquido con conductividad finita, la energía eléctrica se convierte en calor a través de pérdidas resistivas en el material. El calor se genera en la micro escala cuando los electrones de conducción transfieren energía a los átomos del conductor por medio de colisiones.
La transferencia de la energía se realiza a nivel de las moléculas: la interacción de la corriente de electrones con los iones o con los átomos de la parte del conductor de la energía permanece en este último. El efecto térmico lo obtienen los cables con el movimiento más rápido de las partículas conductoras y su energía interna aumenta y se transforma en calor.
Para lograr entender cómo funciona el efecto Joule, debemos empezar explicando qué es el calor. El calor es el desprendimiento de energía por parte de un sistema que se origina como una consecuencia del movimiento y de las partículas que lo componen.
El efecto Joule ocurre cuando se da el desprendimiento de calor estimulado por el movimiento de los electrones, o lo que conocemos normalmente, la corriente eléctrica por un material determinado. Además, el efecto joule va a depender de varios aspectos, los cuales son:
La intensidad de corriente: se refiere al número de electrones por unidad de tiempo. Cuanto menor sea la resistencia y mayor sea la diferencia de potencial, habrá más cantidad de electrones en movimiento en una unidad de tiempo.
La resistencia: es la oposición de un elemento al paso de los electrones por el mismo. Cuanto mayor sea la resistencia, mayor será el número de obstáculos que se presenten en el camino del electrón.
La diferencia de potencial o voltaje: los átomos son los encargados de atraer a los electrones del polo positivo al negativo, generando movimiento.
Tiempo: entre mayor tiempo transcurra la cantidad de calor que ha sido generada aumenta y por eta razón también influye.
Potencia: se refiere a la influencia de la resistencia, la intensidad y la diferencia de potencial de un circuito.
En la ley de Joule o efecto Joule, la energía térmica se representa por medio de la letra E (en Joules o Julios) y esta energía térmica es disipada por un conductor eléctrico de resistencia, el cual es representada por la letra R (ohm) y que es atravesado por una corriente de intensidad I (medida en amperios) durante un tiempo t. Esta explicación se puede representar por medio de la siguiente fórmula:
La energía térmica o en otras palabras el calor, representado por la letra E va a depender de 3 diferentes factores que son los siguientes:

La intensidad I de la corriente (el cual es considerado como el factor más importante ya que está al cuadrado).

El tiempo t durante el cual fluye la corriente.

Resistencia R del conductor.

Aplicaciones del efecto Joule

En la vida práctica, el efecto joule es aplicado en los diferentes artefactos eléctricos que utilizamos por lo general en nuestros hogares con calentadores eléctricos que aprovechan aprovechan este efecto calorífico. También se aplica este principio a la lámpara incandescente la cual funciona cuando el filamento elevado a muy alta temperatura emite luz.
También se puede aplicar a los secadores de pelo por ejemplo, ya que estos disponen en su interior de una serie de resistencias que se van calentando poco a poco mientras se da el paso de la corriente eléctrica, haciendo que el aire que logra salir de ellos sea caliente.

Ejemplos:
Algunos ejemplos del efecto joule los podemos encontrar en:
Una bombilla ordinaria.
Dispositivos de calefacción.
Fusible en el apartamento.
Calentadores de las cocinas eléctricas.
El arco que es usado para la soldadura de estructuras de metal.

Para comprender mejor el tema de la Ley de Joule, podemos analizar la fórmula que utilizaremos para resolver los diversos ejercicios que expondremos aquí mismo. Matemáticamente nuestra expresión es de esta forma:

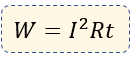
Fórmula del efecto Joule

Dónde:

W = Cantidad de Calor (expresada en Joules)

I = Intensidad de Corriente (expresada en Amperes)

R = Resistencia Eléctrica (expresada en Ohms)

t = Unidad de tiempo (expresado en segundos)

Por lo general como se trata de una pérdida de calor, se suele utilizar las unidades de Caloría, y no la de Joules. Por lo que al realizar nuestra conversión de unidades, obtenemos una nueva fórmula:

$\displaystyle 1J\left( \frac{0.24cal}{1Joule} \right)=0.24cal$

Es decir, que nuestra fórmula tomará la siguiente forma:

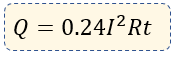
Fórmula de la ley de Joule

Dónde:

Q = Cantidad de Calor (expresada en Calorías).

EJERCICIOS RESUELTOS

Problema 1.- Por el embobinado de un motor eléctrico circulan 5 amperes al estar conectado a una diferencia de potencial de 220 Volts, ¿Qué calor genera en dos minutos?

Solución:

Al circular corriente a través del embobinado del motor eléctrico, este producirá de alguna forma calor. La pregunta que nos hace el problema es saber qué cantidad de calor se genera en dos minutos, para ello coloquemos nuestros datos:

Datos:

$\displaystyle I=5A$

$\displaystyle V=220V$

$\displaystyle t=2\min$

Lo primero que haremos, será convertir los minutos a segundos

$\displaystyle t=2\min \left( \frac{60s}{1\min } \right)=120s$

Ahora debemos encontrar el valor de la resistencia, para ello aplicamos la Ley del Ohm

$\displaystyle I=\frac{V}{R}$

Despejando a “R”

$\displaystyle R=\frac{V}{I}$

Sustituyendo datos:

$\displaystyle R=\frac{V}{I}=\frac{220V}{5A}=44\Omega$

Ahora si podemos sustituirlo en nuestra fórmula:

$\displaystyle Q=0.24{{\left( 5A \right)}^{2}}\left( 44\Omega \right)\left( 120s \right)=31680cal$

Es decir que se disipó en calor un valor aproximado de 31680 calorías en dos minutos.

Problema 2.- Por la resistencia de 60Ω de un radiador eléctrico circula una corriente de 9A al estar conectado a una diferencia de potencial de 120 V. ¿Qué cantidad de calor produce en 8 minutos?

Solución:

A diferencia del ejercicio anterior, en este problema si contamos con el valor de la resistencia, y los demás datos necesarios para la resolución correcta del ejemplo, entonces vamos a recopilar nuestros datos y ver la manera de como introducirlos en la fórmula sin problema alguno.

Datos:

$\displaystyle R=60\Omega$

$\displaystyle I=9A$

$\displaystyle V=120V$

$\displaystyle t=8\min$

Lo primero que podemos observar es que los minutos deben pasarse a segundos, para ello aplicamos el factor de conversión y convertimos:

$\displaystyle t=8\min \left( \frac{60s}{1\min } \right)=480s$

Ahora si podemos hacer uso de la fórmula la ley de Joule

$\displaystyle Q=0.24{{\left( 9A \right)}^{2}}\left( 60\Omega \right)\left( 480s \right)=559872cal$

Lo que nos daría un total de 559,872 Calorías que se produce en 8 minutos.

Problema 3.- Determinar el calor desarrollado en tres minutos por un cautín para soldar cuya potencia es de 180 Watts

Solución:

A diferencia de los ejemplos anteriores, en este caso no contamos con el valor de la resistencia, corriente o resistencia. Solamente tenemos el dato del tiempo y de la potencia. Pero si analizamos bien nuestra fórmula, sabremos que es un problema fácil de resolver. Recopilemos nuestros datos.

Datos.

$\displaystyle P=180W$

$\displaystyle t=3\min$

Antes de comenzar, primero pasaremos los minutos a segundos

$\displaystyle t=3\min \left( \frac{60s}{1\min } \right)=180s$

Sabemos por el tema de Potencia Eléctrica que la potencia es el cuadrado de la corriente por el voltaje, entonces:

$\displaystyle P={{I}^{2}}R$

Si sustituimos la fórmula en la Ley de Joule, obtenemos:

$\displaystyle Q=0.24{{I}^{2}}Rt=0.24Pt$

$\displaystyle Q=0.24Pt$

Sustituyendo los datos en la fórmula:

$\displaystyle Q=0.24Pt=0.24\left( 180W \right)\left( 180s \right)=7776cal$

Por lo que obtenemos un total de 7,776 calorías.

ACTIVIDAD

Utilizando las formulas de la ley de Ohm, resuelva:

Hallar la corriente que pasa por el filamento de un pequeño foco que tiene una resistencia de 200Ω, alimentado por una batería AA de 1.5 Volts.
Hallar el Voltaje aplicado al filamento de un foco de resistencia 138 Ω por el cual pasa una corriente de 0.066 Amp.
Determinar la Resistencia de un filamento por el cual pasa una Corriente de 3.8 mA aplicándole un Voltaje de 6 Volts.
Si una batería AAA tiene un voltaje de 1.5. Volts y el filamento de una lámpara tiene 180 Ω de resistencia ¿Qué corriente circulará por el filamento?.
Qué Voltaje se aplicó al filamento de un foco de resistencia 0 .586 kΩ por el cual pasó una corriente de 2.567 mA.

utilizando las formulas del EFECTO JOULE, resuelva:

Problema 1- Una plancha eléctrica tiene una resistencia de 35Ω y se conecta durante 25 minutos a una diferencia de potencial de 110V. ¿Qué cantidad de calor produce?

Problema 2- Una plancha eléctrica tiene una resistencia de 35Ω y se conecta durante 25 minutos a una diferencia de potencial de 220V. ¿Qué cantidad de calor produce?

Problema 3.- Una secadora de cabello tiene una resistencia de 25Ω al circular una corriente de 8 Amperes, si está conectado a una diferencia de potencial de 120 V, durante 32 minutos ¿Qué cantidad de calor produce?

Referencias

tomado de:
https://ekuatio.com/la-ley-de-ohm-que-es-aplicaciones-y-ejercicios-triangulo-de-la-ley-de-ohm/
https://www.euston96.com/efecto-joule/
https://www.fisimat.com.mx/ley-de-joule/

física y química 10 y 11 sede Terranova

miércoles, 30 de septiembre de 2020

ACTIVIDAD No. 15 FÍSICA GRADO UNDÉCIMO 2 PERIODO

APLICACIONES DE LA LEY DE OHM Y LA LEY DE JOULE

¿Qué es la ley de Ohm?

Fórmula de la ley de Ohm

Ley de Ohm para calcular la intensidad

Ley de Ohm para calcular el voltaje

Ley de Ohm para calcular la resistencia

Ejercicios resueltos de la ley de Ohm

Ejercicio 1

Ejercicio 2

LEY DE JOULE

¿Qué es el efecto Joule?

Aplicaciones del efecto Joule

No hay comentarios.:

Publicar un comentario