Estaré enviando a ustedes vía whatsapp el link de la clase en línea para explicar las dudas acerca de esta temática, la plataforma sugerida para dicha clase es zoom.
la clase en línea esta programada para el día miércoles 3 y 5 de junio a las 3 p.m.
les envío un fuerte abrazo, espero que todos se encuentren bien. Los extraño mucho.🙅🙅🙅
OSCILACIONES Y ONDAS MECÁNICAS (PARTE I: MOVIMIENTO ARMÓNICO SIMPLE)
MOVIMIENTO OSCILATORIO:
Es aquel movimiento en el cual el cuerpo se mueve hacia uno y otro lado respecto a una posición de equilibrio, es decir, efectúa un movimiento de vaivén.
El movimiento oscilatorio es un movimiento en torno a un punto de equilibrio estable. Este puede ser simple o completo. Los puntos de equilibrio mecánico son, en general, aquellos en los cuales la fuerza neta que actúa sobre la partícula es cero.
Decimos que un cuerpo oscila o vibra cuando se mueve de forma periódica entorno a una posición de equilibrio debido al efecto de fuerzas restauradoras. Las mágnitudes características de un movimiento oscilatorio o vibratorio son:
Periodo (T): El tiempo que tarda de cumplirse una oscilación completa. Su unidad de medida en el Sistema Internacional es el segundo (s).
Frecuencia (f): Se trata del número de veces que se repite una oscilación en un segundo. Su unidad de medida en el Sistema Internacional es el hertzio (Hz)
Tipos de vibraciones
Existen dos tipos de vibraciones u oscilaciones atendiendo a las fuerzas que actúan:
Oscilaciones libres: Cuando sobre el cuerpo no actúan fuerzas disipativas. El cuerpo no se detiene, oscila indefinidamente, al no haber una fuerza que contrarreste el efecto de la fuerza restauradora
Oscilaciones amortiguadas: Cuando actúan fuerzas disipativas (como por ejemplo la fuerza de rozamiento o de fricción) que acaban por hacer que las oscilaciones desaparezcan. El cuerpo acabará retornando a la posición de equilibrio
MOVIMIENTO ARMÓNICO SIMPLE (M.A.S.)
Es aquel movimiento oscilatorio que se repite en intervalos iguales de tiempo y ademas se realiza en una trayectoria con tendencia a la línea recta.
Decimos que una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando vibra bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio. Decimos, entonces, que dicho cuerpo es un oscilador armónico.
Características del movimiento armónico simple:
Vibratorio: El cuerpo oscila en torno a una posición de equilibrio siempre en el mismo plano
Periódico: El movimiento se repite cada cierto tiempo denominado periodo (T). Es decir, el cuerpo vuelve a tener las mismas magnitudes cinemáticas y dinámicas cada T segundos.
A la partícula o sistema que se mueve según un movimiento armónico simple se les denomina oscilador armónico.
Magnitudes del movimiento armónico simple
Elongación, X: Representa la posición de la partícula que oscila en función del tiempo y es la separación del cuerpo de la posición de equilibrio. Su unidad de medidas en el Sistema Internacional es el metro (m)
Amplitud, A: Elongación máxima. Su unidad de medidas en el Sistema Internacional es el metro (m).
Frecuencia. f: El número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.
Periodo, T: El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
LEY DE HOOKE
La ley de elasticidad de Hooke o ley de Hooke, establece la relación entre el alargamiento o estiramiento longitudinal y la fuerza aplicada. La elasticidad es la propiedad física en la que los objetos con capaces de cambiar de forma cuando actúa una fuerza de deformación sobre un objeto. El objeto tiene la capacidad de regresar a su forma original cuando cesa la deformación. Depende del tipo de material. Los materiales pueden ser elásticos o inelásticos. Los materiales inelásticos no regresan a su forma natural.
Constante del resorte (K):
Se tiene un resorte al que se le aplica una fuerza de tensión F, de manera que el resorte se alarga una distancia ∆X.
Según la Ley de Hooke, la fuerza aplicada debe ser proporcional a la deformación producida y la constante de proporcionalidad es K, la cual es específica para cada resorte. Esta constante dependerá no sólo del tipo de material del que está hecho el resorte (acero, aluminio, hierro, etc.) sino del diámetro del alambre e incluso de la distancia entre dos vueltas consecutivas de la hélice que forma el resorte y el diámetro de la misma.
La Ley de Hooke para el resorte se escribe:
F = K.∆X
Ejemplo práctico: calcula la constante recuperadora de un resorte.
Colgamos sucesivamente masas de 2, 4 y 6 kg del muelle y observamos que los diferentes alargamientos son proporcionales.
La fuerza aplicada en los diferentes casos es el peso: F = P = mg
Sustituyendo en la formula, obtenemos que la constante de proporcionalidad es:
tener en cuenta que:
1cm=0,01m
2cm=0,02m
3cm=0,03m
K = F/∆X
K = mg/∆X
Por lo tanto,
K = (2kg* 9,8m/s2 )/ 0,01m = 1960 N/m
K = (4kg* 9,8m/s2 )/ 0,02m = 1960 N/m
K = (6kg* 9,8m/s2 )/ 0,03m = 1960 N/m
PERIODO DE OSCILACIÓN
Otro ejemplo de Movimiento Armónico Simple es el sistema masa-resorte que consiste en una masa “m” unida a un resorte, que a su vez se halla fijo a una pared, como se muestra en la figura. Se supone movimiento sin rozamiento sobre la superficie horizontal.
El resorte es un elemento muy común en máquinas. Tiene una longitud normal, en ausencia de fuerzas externas. Cuando se le aplican fuerzas se deforma alargándose o acortándose en una magnitud “x” llamada “deformación”. Cada resorte se caracteriza mediante una constante “k” que es igual a la fuerza por unidad de deformación que hay que aplicarle. La fuerza que ejercerá el resorte es igual y opuesta a la fuerza externa aplicada (si el resorte deformado está en reposo) y se llama fuerza recuperadora elástica.
Dicha fuerza recuperadora elástica es igual a :
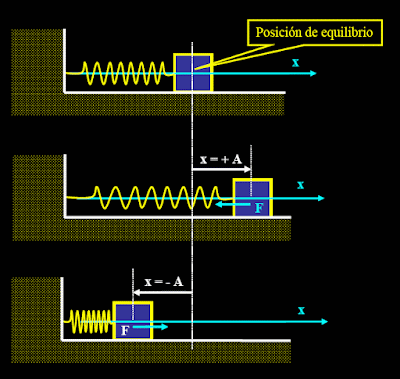
En el primer dibujo tenemos el cuerpo de masa “m” en la posición de equilibrio, con el resorte teniendo su longitud normal.
Si mediante una fuerza externa lo apartamos de la misma (segundo dibujo), hasta una deformación “x = + A” y luego lo soltamos, el cuerpo empezará a moverse con M.A.S. oscilando en torno a la posición de equilibrio. En este dibujo la fuerza es máxima pero negativa, lo que indica que va hacia la izquierda tratando de hacer regresar al cuerpo a la posición de equilibrio.
Llegará entonces hasta una deformación “x = -A” (tercer dibujo). En este caso la deformación negativa indica que el resorte está comprimido. La fuerza será máxima pero positiva, tratando de volver al cuerpo a su posición de equilibrio.
A través de la Segunda Ley de Newton relacionamos la fuerza actuante (recuperadora) con la aceleración a(t).
PÉNDULO SIMPLE
El pendulo simple es aquel dispositivo que está constituido por una masa de pequeñas dimensiones, suspendida de un hilo inextensible y de peso despreciable.
Un péndulo simple es una masa puntual m suspendida verticalmente mediante una cuerda o hilo inextensible de masa despreciable y longitud l.
Cuando el péndulo se encuentra en reposo, en vertical, permanece en equilibrio ya que la fuerza peso es contrarrestada por la tensión en la cuerda.
Una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando oscila bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio.
Un péndulo simple se comporta como un oscilador armónico cuando oscila con amplitudes pequeñas. La fuerza restauradora es la componente tangencial del peso, de valor Pt, y la aceleración del péndulo es proporcional al desplazamiento pero de sentido contrario, con expresión:
Donde:
- a: Aceleración del péndulo. Depende de la distancia a la posición de equilibrio x. Su unidad de medida en el Sistema Internacional es el metro por segundo al cuadrado ( m/s2 )
- g: Aceleración de la gravedad. Su valor es 9.8 m/s2
- l: Longitud del péndulo. Su unidad de medida en el Sistema Internacional es el metro ( m )
- x: Separación x de la vertical de equilibrio del péndulo. Su unidad de medida en el Sistema Internacional es el metro ( m )
Un oscilador armónico no es más que una partícula que se mueve según un m.a.s. La aceleración que aparece en el péndulo cuando se separa de su posición de equilibrio hace que el péndulo vibre u oscile en torno a su posición de equilibrio. Dichas vibraciones siguen el patrón de un movimiento armónico simple si el ángulo de oscilación es pequeño (no más de 15º o 20º).
Periodo del péndulo simple
El periodo del péndulo simple, para oscilaciones de poca amplitud, viene determinado por la longitud del mismo y la gravedad. No influye la masa del cuerpo que oscila ni la amplitud de la oscilación.
El periodo del péndulo simple es el tiempo que tarda el péndulo en volver a pasar por un punto en el mismo sentido. También se define como el tiempo que tarda en hacerse una oscilación completa. Su valor viene determinado por:
Donde:
- T: Periodo del péndulo. Su unidad de medida en el Sistema Internacional es el segundo ( s )
- l: Longitud del péndulo. Su unidad de medida en el Sistema Internacional es el metro ( m )
- g: Gravedad. Su unidad de medida en el Sistema Internacional es el metro por segundo al cuadrado ( m/s2 )
EJEMPLOS RESUELTOS
ACTIVIDAD
referencias
























No hay comentarios.:
Publicar un comentario